Convex Functions

Convex functions is an important and fundamental class of objective functions in the study of mathematical optimization. Their properties make them the simplest, yet non-trivial, objective functions for optimization. Convex functions are those functions whose local minima is also a global minima. Furthermore, strictly convex functions have at most one local minima, which is also the global minima.

Given that most of the machine learning algorithms end up optimizing some cost function (i.e., objective function), knowing about convexity would help understanding the properties of these algorithms. For example, support vector machines (SVMs), linear regression, ridge regression, and lasso regression generate the convex cost functions, and maximum likelihood estimation of logistic regression generates a concave cost function. On the other hand, neural network based models deal with non-convex optimization (i.e., neither convex nor concave).

This post presents the definition and properties of convex functions.

Convexity

A function is called convex function if the line segment connecting between any two points on the curve lies above the curve. Note the emphasis on any, the statement should hold for all possible pairs of points on the curve. Mathematically, a function $f: X \rightarrow Y$ is said to be convex if:

\[\forall x_1 \neq x_2 \in X, \forall x_i \in [x_1, x_2]:\ \ f(x_i) \le \dfrac{f(x_2) - f(x_1)}{x_2 - x_1} (x_i - x_1) + f(x_1) \\\]

The r.h.s. of the above equation is the $y$ value corresponding to $x_i$ on the line segment joining points $(x_1, f(x_1))$ and $(x_2, f(x_2))$.

Following figure shows the property of convex functions graphically. $y_s$ is the r.h.s. of the inequality and $y_c$ is the l.h.s. This should hold for the whole segment and for all such possible segments.

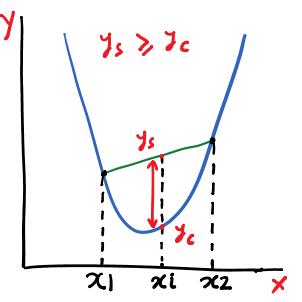
We can simplify the equation by substituting $x_i$ with $t x_1 + (1-t) x_2$ for $t \in [0, 1]$. For $t=0$ and $t=1$, the value of $x_i$ is $x_2$ and $x_1$ respectively. For the other values of $t \in (0, 1)$ , $x_i$ ranges in $(x_1, x_2)$.

\[\forall x_1 \neq x_2 \in X, \forall t \in [0, 0]:\ \ f(t x_1 + (1-t) x_2) \le t f(x_1) + (1-t) f(x_2) \\\]

Note: the above inequality is called Jensen’s inequality.

A function is called strictly convex if:

\[\forall x_1 \neq x_2 \in X, \forall t \in [0, 0]:\ \ f(t x_2 + (1-t) x_1) \lt t f(x_2) + (1-t) f(x_1) \\\]

We can symmetrically define concave functions as those where the line segment lies below the curve. Similarly, we can also define strictly concave functions.

Properties

• $f(x)$ is a convex function $iff$ $-f(x)$ is concave function.
• For strictly convex functions, local minimum is also the global minimum.
• For convex functions there can be multiple local minimums, however, all of them would function would map them to same value. Moreover, these would also be the global minimums.
• Iterative algorithms like Gradient descent would always approximate the global minimum, as long as other requirements of Gradient descent are met, e.g., existence of gradient.
• All linear functions are both convex and concave. Requirements of convex and as well as concave functions are met for linear functions. Though, they are neither strictly convex nor strictly concave.
• If a function is of single variable and its twice derivative exists, then it is greater than or equal to zero for the whole domain for concave functions. Symmetrically, for concave functions, its twice derivative is less than or equal to zero for all values in domain. For the strict counterparts, equality with zero is omitted.