Monte Carlo Methods

Monte Carlo method is an important technique to reason about probabilistic systems (or deterministic systems that can be modeled as probabilistic systems). It is used to solve the problems that involve uncertainty, or are intractable to solve using the standard methods, e.g., interacting particles system. Given that the world is full of problems with uncertainty, Monte Carlo methods have been successfully used in an endless list of disciplines.

The primary idea of Monte Carlo method is repeated random sampling of the various probabilistic inputs, and estimating the required properties based on the corresponding generated outputs. For example, one can use Monte Carlo to find the long term expected earnings that can be made by a casino from a specific type of Roulette wheel. The earning made by the casino is a function of the observed values of the various spins of the Roulette wheel, which is the probabilistic input of the system. Monte Carlo simulation would consider a number of Roulette games where in the each game: the result of the wheel is drawn from a uniform random distribution, and based on the result, the casino’s earning is computed. The final result is the sum of the earnings of all the games. The law of large numbers will help establish the fact the simulation indeed converges to the desired computation.

It is also possible to model a deterministic problem as a probabilistic computation and then using Monte Carlo method to solve the same. For example, we can compute the value of pi by randomly throwing balls in a 2x2 square bounding a circle of radius 1. We compute the fraction of balls land in the circle. After a fairly large number of trials, the value will converge to the value of pi/4.

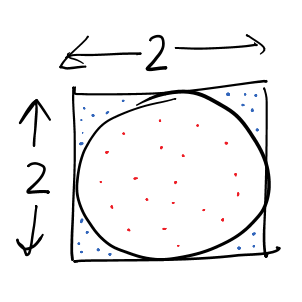
In the above figure, the dots (balls) are placed randomly, drawn from a uniform distribution. We count the number of points in the circle (red) and divide it by the total balls dropped (blue+red). Following python program performs the same Monte Carlo simulation:

import random

points_in = 0
N = 1000000
for step in range(N):
    x = random.uniform(-1, 1)
    y = random.uniform(-1, 1)
    if x**2 + y**2 < 1: # in the circle
        points_in += 1
print(4*points_in/N)

The output of the program is non-deterministic and it is not guaranteed to return the same value on each run. Some of the values that I got are: 3.1406, 3.143188, 3.142416. Note that the values are close to the value of pi.

Stick to this space for a detailed analysis and reasoning of this simulation.